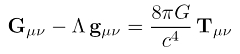Pluto hat geschrieben:Halman hat geschrieben:Dies verstehe ich so, dass die Energie eines echten Vakuums scharf 0 beträgt, obgleich die Feldstärke der Quantenfelder unscharf ist und daher Feldfluktuationen vorliegen.
Und wie passt dann bspw. die Dunkle Energie in dieses Modell? Gibt es ein NICHTS ausserhalb des uns bekannten Vakuums mit seinen Quantenfeldern?
Ich bin davon überzeugt, dass eine neue Physik her muss, bevor wir diese und andere Beobachtungen im Universum erklären können.
Dies wäre dann wohl eine vollständige Theorie der Quantengravitation. Es gibt viele Experten auf diesem Gebiet - nun fehlt ihnen nur noch eine vollständige Theorie.

Das Problem dabei besteht schlicht darin, dass die Energie "dunkel" ist. Wir schlussfolgern über die Wirkung auf eine unsichtbare Ursache. Man könnte sagen, wir glauben an eine unsichtbare Kraft, welches das ganze Universum beeinflusst (sorry, diese Forumlierung war einfach zu verlockend

). Daher tappen wir bei den
Erklärungsversuchen auch im Dunkeln.
Bereits Einstein vermutete eine der Gravitation entgegengesetzte Kraft. Daher fügte er seiner ART-Feldgleichung die
Kosmologische Konstante in Form eines Λ-Terms hinzu, um das von ihm seinerzeit favorisierte ästhetisch schöne, statische Universum plausibel erklären zu können. Als dann Edwin P. Hubble die Rotverschiebung ferner Galaxien beobachtete, die auf ein expandierendes Universum hinwies, verwarf er diese Idee m. W. als seine größte Eselei und setzte er den Λ-Term auf 0.
Als dann 1998 die Beobachtung ferner Supernovae vom Typ Ia (dessen absolute Leuchtkraft bekannt ist) darauf schließen ließ, dass unser Universum in den letzten 5 bis 6 Milliarden Jahren beschleunigt expandiert, erinnerte man sich an den Λ-Therm, den Einstein auf 0 gesetzt hatte. Nach aktuellen Messungen scheint der Wert für den Λ-Term [rätselhaferweise] bei 0,683 zu liegen. Hierfür wurde der Begriff
Dunkle Energie geprägt. Die beschleunigte Expansion wird also dadurch erklärt, indem ΩΛ ≈ 0.683 gesetzt wird, d.h. dass etwa 68,3% der Gesamtenergie des Universums aus Dunkler Energie besteht.
Hier mal die einsteinische Feldgleichung mit Kosmologischer Konstante
Λ:
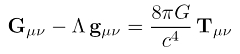
Dabei wird
Λ mit dem metrischen Tensor
gμν multipiziert. Ist
Lambda positiv, überwiegt die Antigravitation, ist
Λ negativ, überwiegt die Gravitation.
Für die raumzeitliche Krümmung eines Gebiets ist der Impuls- und Energiegehalt in einem raumzeitlichen Gebiet entscheidend. Global kommt es also auf die Energiedichte an, insbesondere auf das Verhältnis von Materie (baryonische - und Dunkle Materie) mit positiver Energiedichte, die daher gravitativ wirkt, und Dunkler Energie, die antigravitativ wirkt.
Im Artikel
Kosmologische Konstante, unter dem Abschnitt
Ist Λ konstant?, wird hierzu ausgesagt:
Eine ganz andere Frage ist, ob der Zahlenwert, der mit Λ assoziiert ist, zu allen Zeiten gleich ist oder ob es einen Spielraum für Variationen gibt.
Die Theorie lässt diesen Spielraum zu: der Lambda-Term muss nicht notwendig konstant sein. Doch die aktuellen Beobachtungen der experimentellen Kosmologie lassen diesen Spielraum nicht zu - zumindest nicht in den letzten neun Millarden Jahren. Woher wissen das die Beobachter? Sie vermessen eine Vielzahl von hochrotverschobenen Supernovae vom Typ Ia mit dem Weltraumteleskop Hubble (Riess et al. 2004, astro-ph/0402512; bestätigt 2006). Diese Daten zeigen, dass Einstein mit seiner Intuition Recht hatte und tatsächlich eine kosmologische Konstante vorliegt, die zeitlich unveränderlich ist. Big Crunch und Big Rip erscheinen nach diesen Daten als sehr unwahrscheinliche Szenarien für die Zukunft des Universums.
Bei der Dunklen Energie
scheint es sich demnach tatsächlich um Konstante zu handeln.
Laut den neuesten Messungen der Raumsonde PLANCK ist unser Universum ≈ 13,82 Mrd. Jahre alt. Im Link findest Du eine PDF-Datei mit einer Grafik, in der die aktuellen Daten den inzwischen veralteten Daten gegenübergestellt werden:
http://www.sterne-und-weltraum.de/alias ... se/1189337
Unschärferelation:
Die Unschärferelation beschreibt
kein Messproblem, sondern eine fundamentale Eigenschaft von Quantenobjekten. Die Formel für die Heisenberg'sche Unschärferelation lautet:
Δ
x * Δ
p >
ħ / 2
D.h, je genauer oder schärfer Δ
x bestimmt wird (also je genauer das Quantenobjekt lokalisiert ist), je unschärfer ist der Wert für den Impuls Δ
p (umgekehrt gilt das Gleiche).
Da den Quantenobjekten also die Eigenschaften fehlen, dass Ort und Impuls gleichermaßen „scharf“ bestimmt sind (ganz anders, als in unserer mesokosmischen Erfahrungswelt), ist es auch irreführend, ihnen solche Eigenschaften zuschreiben zu wollen.
@Janina
Danke für Deine Erklärung.