Quantenmechanische Gedanken zum Urknall
#181 Re: Quantenmechanische Gedanken zum Urknall
Auch wenn nicht zutreffend: Das bewerte ich mal als Lob.

#182 Re: Quantenmechanische Gedanken zum Urknall
Wenn du das als Lob bewertest, vermute ich, dass du die Bedeutung von Opportunismus nicht verstanden hast.Scrypt hat geschrieben:Auch wenn nicht zutreffend: Das bewerte ich mal als Lob.
Der Naturalist sagt nichts Abschließendes darüber, was in der Welt ist.
#183 Re: Quantenmechanische Gedanken zum Urknall
Du irrst erneut.Pluto hat geschrieben:Wenn du das als Lob bewertest, vermute ich, dass du die Bedeutung von Opportunismus nicht verstanden hast.Scrypt hat geschrieben:Auch wenn nicht zutreffend: Das bewerte ich mal als Lob.
Spielt hier aber ohnehin keine Rolle.
#184 Re: Quantenmechanische Gedanken zum Urknall
Da bin ich anderer Meinung. Zwar ist die Messung eindeutig, aber erst durch die Messung erhalten wir ein eindeutiges Messergebnis, welches NICHT vorhersehbar war.Pluto hat geschrieben:@ Halman
So wie ich es verstehe, ist die "Kopenhagener Deutung" der Qantenphysik nicht determiniert. Der Kollaps der Wellenfunktion führt aber zu einer eindeutigen Messung, sodass sich Kollaps und Kopenhagener Deutung einander sozusagen widersprechen.
Zwar ist das Interferenzmuster beim Doppelspaltexperiment kausal vorhersehbar, aber der exakte Detektionsort eines Teilchens ist objektiv unbestimmt. Ähnlich verhält es sich mit einem radionaktiven Isotop. Zwar ist die Halbwertzeit bestimmbar, aber der Zerfall eines einzelnen Atoms geschiet vollkommen zufällig.
Ganz anders als bspw. im Billard-Spiel unserer Erfahrungswelt. Bei determinierten Systemen ist es theoretisch möglich, jeden Zustand zu berechnen, sofern man alle Daten über einen Zustand des Gesamtsystems zu einer gegebenen Zeit t0 hat. So könnte z.B. ein Cyborg (hier kommt durch, dass ich Summer-Glau-Fan bin) einen Stoß im Billard-Spiel berechnen, sieh selbst
Diesen widerspricht die Quantenmechanik jedoch sehr hartnäckig. Um es mal scherzhaft auszudrücken: Quantenobjekte scheinen sich für den gesunden Menschenverstand nicht zu interessieren.
Gem. der Quantenmechanik (QM) lässt sich das Verhalten von Quantenobjekten nicht eindeutig bestimmen, ihr Verhalten ist objektiv zufällig (die Schrödingergleichung erlaubt lediglich eine statistische Wahrscheinlichkeit zu berechen). Um den daraus resultierenden Interdeterminismus zu umgehen, erdachte Einstein sich verborgene Parameter die lokal und unmessbar das Verhalten von Quantenobjekten determinieren.
Gem. so einer lokal-realistischen Theorie geht der Zufall in der Quantenmechanik (QM) nur auf Datenmangel zurück: Demzufolge wäre die QM als eine unvollständige Theorie anzusehen.
Allerdings legen alle bekannten Daten einen objektiven Zufall nahe, der nicht auf Datenmangel zurückzuführen ist (Kopenhagener Kollaps). So verschwindet beim Doppelspaltexperiment das Interferenzmuster, sobald man durch die Messung die Positionen der Quantenobjekte bestimmt. Dass lässt sich dadurch erklären, dass durch die Messung die Wellenfunktion des Quantenobjektes kollabiert.
Die Wellenfunktion erweist sich als außgesprochen "filigranes Gebilde" (bitte nicht wörtlich nehmen, hier bediene ich mich einer anschaulichen Sprache), sie zerplatzt wie eine Seifenblase, sobald wir sie durch Beobachtung/Messung antasten.
Die Wellenfunktion |ψ> beschreibt den Gesamtzustand, der alle Einzelzustände |Ï•n> umfasst. Um es einfacher zu machen, erlaube ich mir hier mal die Freiheit, Dr. Bertlmanns Socken als verschränkte Quantenobjekte zu betrachten.
Die Wellenfunktion |Ψ> umfasst alle Einzelzustände |φ>, in diesem Fall also die Sockenfarben:
|φgrün>
|φpink>
Dann würde die Wellenfunktion den Gesamtzustand |Ψbunt> umfassen. Wird das Quantenobjekt "Socke" gemessen, wird aus der bunten Vielfallt, die in |Ψbunt> enthalten ist, objektiv zufällig ein Farbenzustand ausgewählt, z.B. |φgrün>. Wie können |Ψbunt> nicht beobachten, sondern immer nur mit einer statistischen Wahrscheinlichkeit eine der Einzelzustände |φgrün> oder |φpink>.
Quantenobjekte sind also keine Teilchen im klassischem Sinne, sondern, sondern sie erscheinen uns wie seltsame "Welle-Teilchen", obgleich es sich weder um "klassische Teilchen" noch "klassische Wellen" handelt.
Diesbezüglich verweise ich die Seiten 64 bis 75 aus Skurrile Quantenwelt. Darin wird es plausibel und nachvollziehbar erklärt.
Die Unschärfe von Teilchen ist eine fundamentale Eigenschaft und geht keinesfalls auf ein Messproblem zurück. Die Formel für die Heisenberg'sche Unschärferelation lautet:
Δx * Δp > ħ / 2
D.h, je genauer oder schärfer Δx bestimmt wird (also je genauer es lokalisiert ist), je unschärfer ist der Wert für den Impuls Δp (umgekehrt gilt das Gleiche).
Da den Quantenobjekten (Teilchen) also die Eigenschaften fehlen, dass Ort und Impuls gleichermaßen „scharf“ bestimmt sind (ganz anders, als in unserer mesokosmischen Erfahrungswelt), ist es auch sinnfrei, ihnen solche Eigenschaften zuschreiben zu wollen.
Im Doppelspaltexperiment zeigt sich, dass kohärentes Licht (Photonen) ebenso wie Fullerenmoleküle (60 bis 94 Atome), welche die beiden Spalten passieren, auf der dahinter liegenden Detektorplatte ein Interferenzmuster bilden, sich also wie Wellen verhalten.
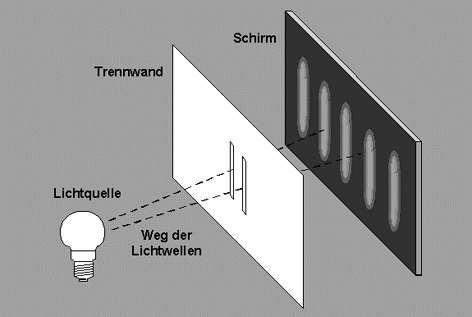
Grafikquelle
Erklärt wird dies mittels einer Wellenfunktion (Formelzeichen ψ), über die man das Verhalten von Quantenobjekten beschreibt. Bei der Messung (z. B. auf dem Detektorschirm) kollabiert nach der Kopenhagener Deutung diese Wellenfunktion und wir messen ein positioniertes Teilchen (Kollaps der Wellenfunktion).
Es verhielt sich aber nicht mechanisch, wie man es von einem Teilchen erwarten würde, auch nicht wie eine Welle, denn diese könnte man nicht als punktförmiges Teilchen messen, sondern eben wie ein Quantenobjekt, welches sich wie eine Welle verhält, solange man nicht hinguckt, aber bei der Messung als Teilchen registrierst wird. Es scheint fast so, als würden sich die Quantenobjekte ihres Wellencharakters schämen.
Wo man es als Teilchen registriert, ist im Voraus nicht bestimmbar. Man kann aber eine statistische Wahrscheinlichkeit dafür angeben (das mathematische Verfahren ersann Erwin Schrödinger, der Mann mit der „Katze“), mit dem man im Falle des Doppelspaltexperiments als wahrscheinliche Detektions-Orte für Quantenobjekte das Interferenzmuster erhält. Dies ist objektiver Zufall.
Nun könnte man natürlich annehmen, dass hier irgendwelche verborgenen Parameter den Detektionsort eines Teilchens (ob nun Photon oder Fullerenmolekül) festlegen, doch lokale verborgene Parameter wurden durch die Bell'sche Ungleichungen falsifiziert.
Es verhält sich eben NICHT so wie bei Dr. Bertlmanns Socken, bei denen ja die Sockenfarben von vorn herein feststehen und nicht erst durch die Beobachtung festgelegt werden.
Was für den Detektionsort von Quantenobjekten auf dem Detektorschirm gilt, gilt auch für die Spinorientierung.
*farbliche Hervorhebung von mirZitat aus Skurrile Quantenwelt:
Nach der Theorie der Quantenmechanik besitzt das Teilchen, solange es nicht gemessen wird, überhaupt keine konkrete Spinrichtung. Es befindet sich anfangs (je nach Präparation) in einer Superposition aus mehreren, wenn nicht sogar unendlich vielen, möglichen Spinorientierungen. In Diracscher Notation schreibt sich der quantenmechanische Zustand des Teilchens daher im Superpositionszustand als
|Ψ> = a |↑> + b |↓>
Einzige "Nische" bleibt die Bohm'sche Mechanik, welche nicht-lokale verborgene Parameter postuliert, die aber als wenig wahrscheinlich gilt.
Zwar ist die Bohm'sche Mechanik ebenso wie die bohr'sche Quantenmechanik mit den experimentellen Ergebnissen vereinbar. Doch problematisch wird es, wenn man eine "bohm'sche Quantenfeldtheorie" konstruieren will, da eine determinsitsche Beschreibung laut Wikipedia bisher nur für bosonische Quantenfelder gelang.
Alle Teilchen lassen sich in zwei Gruppen unterteilen:
- Bosonen (Teilchen mit ganzzahligem Spin, Eich-Bosonen, z.B. Photonen): Laser lassen sich beliebig bündeln.
- Fermionen (Teilchen mit halbzahligem Spin, Materieteilchen, wie Elektronen und Quarks): Zwei gleiche Fermionen können nicht am gleichen Ort sein.
Bosonen lassen sich gem. der QFT als Anregungen bosonischer Quantenfelder verstehen.
Die Fermionen unterliegen dem Pauli-Prinzip. Dieses Prinzip ist dafür verantwortlich, dass sich in der K-Schale der Atome² nur zwei Elektronen mit gegensätzlichen Spin befinden können. Ein drittes Elektron hätte wieder den selben Spin wie eines der anderen und dieses duldet das Pauli-Prinzip nicht.
Übrigens, in Supraleitern bilden sich Elektronen-Paare, die gemeinsam als Bosonen auftreten. Dies erlaubt einen widerstandfreien Elektronen-Fluss.
Mehr dazu in Elementarteilchen.info
Ein weiteres Problem der Bohm'schen Mechanik besteht darin, dass für eine relativistische Erweiterung ein ausgezeichnetes Bezugssystem eingeführt werden müsste, welches in der Relativitätstheorie nicht existiert.
²Das bohr'sche Atommodell v. 1913 ist nur ein Arbeitsmodell und keine Beschreibung der physikalischen Realität.
Tja, ein Proton müsste man sein: Dann würde man die Quantenphysik verstehen, wäre immer positiv drauf und hätte eine nahezu unendliche Lebenszeit:-) - Silvia Arroyo Camejo
#185 Re: Quantenmechanische Gedanken zum Urknall
Beim Doppelspaltexperiment ist das Messergebnis sogar berechenbar.Halman hat geschrieben:Da bin ich anderer Meinung. Zwar ist die Messung eindeutig, aber erst durch die Messung erhalten wir ein eindeutiges Messergebnis, welches NICHT vorhersehbar war.Pluto hat geschrieben:@ Halman
So wie ich es verstehe, ist die "Kopenhagener Deutung" der Qantenphysik nicht determiniert. Der Kollaps der Wellenfunktion führt aber zu einer eindeutigen Messung, sodass sich Kollaps und Kopenhagener Deutung einander sozusagen widersprechen.
Eben darum ist die Kopenhagener Deutung nicht deterministisch.Halman hat geschrieben:Zwar ist das Interferenzmuster beim Doppelspaltexperiment kausal vorhersehbar, aber der exakte Detektionsort eines Teilchens ist objektiv unbestimmt.
Wir können die Halbwertszeit exakt angeben. Warum sollte es wichtig sein, welche Atome "überleben"; si sind doch alle gleich und gleichwertig.Halman hat geschrieben:Ähnlich verhält es sich mit einem radionaktiven Isotop. Zwar ist die Halbwertzeit bestimmbar, aber der Zerfall eines einzelnen Atoms geschiet vollkommen zufällig.
Das stimmt.Halman hat geschrieben:Diesen widerspricht die Quantenmechanik jedoch sehr hartnäckig. Um es mal scherzhaft auszudrücken: Quantenobjekte scheinen sich für den gesunden Menschenverstand nicht zu interessieren.
Obwohl etwa 70% der weltweiten Industrieproduktion Quanteneffekte verwendet, wissen noch sehr wenig darüber was sich wirklich in diese sub-nano Welt abspielt.
Wir können die Quantenwelt statistisch erfassen. Das ist in meinen Augen erstens schon sehr viel und vermutlich auch die einzige Möglichkeit sie zu erklären.Halman hat geschrieben:Gem. der Quantenmechanik (QM) lässt sich das Verhalten von Quantenobjekten nicht eindeutig bestimmen, ihr Verhalten ist objektiv zufällig (die Schrödingergleichung erlaubt lediglich eine statistische Wahrscheinlichkeit zu berechen).
Unsere experimentellen Mittel sind aber auch filigran geworden. Siehe den dynamischen Casimir-Effekt, wo Licht aus dem Nichts erzeugt wird.Halman hat geschrieben:Die Wellenfunktion erweist sich als außgesprochen "filigranes Gebilde" (bitte nicht wörtlich nehmen, hier bediene ich mich einer anschaulichen Sprache), sie zerplatzt wie eine Seifenblase, sobald wir sie durch Beobachtung/Messung antasten.
Energie wird durch die Schwingungen des Spiegels von Außen ins System gepumpt, weshalb die virtuellen Photonen sich in Reale verwandeln können und nicht wieder ins Nichts zurückfallen - so erklärt es der Physiker in dem von mir verlinkten Video.
Eben.Halman hat geschrieben:Nun könnte man natürlich annehmen, dass hier irgendwelche verborgenen Parameter den Detektionsort eines Teilchens (ob nun Photon oder Fullerenmolekül) festlegen, doch lokale verborgene Parameter wurden durch die Bell'sche Ungleichungen falsifiziert.
Ja klar!Halman hat geschrieben:Was für den Detektionsort von Quantenobjekten auf dem Detektorschirm gilt, gilt auch für die Spinorientierung.
Da fehlt was.Halman hat geschrieben:Die Fermionen unterliegen dem Pauli-Prinzip. Dieses Prinzip ist dafür verantwortlich, dass sich in der K-Schale der Atome² nur zwei Elektronen mit gegensätzlichen Spin befinden können. Ein drittes Elektron hätte wieder den selben Spin wie eines der anderen und dieses duldet das Pauli-Prinzip nicht.
Neutronen sind Fermionen, aber ein Neutronenstern besteht aus Trillionen von Neutronen, oder nicht?
Der Naturalist sagt nichts Abschließendes darüber, was in der Welt ist.
#186 Re: Quantenmechanische Gedanken zum Urknall
Ja, als Interferenzmuster. Aber für EINZELNE Quentenobjekte ist es unberechebar. Da können wir nur eine Wahrscheinlichkeit angeben.Pluto hat geschrieben:Beim Doppelspaltexperiment ist das Messergebnis sogar berechenbar.Halman hat geschrieben:Da bin ich anderer Meinung. Zwar ist die Messung eindeutig, aber erst durch die Messung erhalten wir ein eindeutiges Messergebnis, welches NICHT vorhersehbar war.Pluto hat geschrieben:@ Halman
So wie ich es verstehe, ist die "Kopenhagener Deutung" der Qantenphysik nicht determiniert. Der Kollaps der Wellenfunktion führt aber zu einer eindeutigen Messung, sodass sich Kollaps und Kopenhagener Deutung einander sozusagen widersprechen.
Eben (s.o.).Pluto hat geschrieben:Eben darum ist die Kopenhagener Deutung nicht deterministisch.Halman hat geschrieben:Zwar ist das Interferenzmuster beim Doppelspaltexperiment kausal vorhersehbar, aber der exakte Detektionsort eines Teilchens ist objektiv unbestimmt.
Das mag sein, dennoch gilt der Interdeterminsmus der skurrilen Quantenwelt. Dies ist naturphilosophisch meiner Meinung nach von größter Bedeutung.Pluto hat geschrieben:Wir können die Halbwertszeit exakt angeben. Warum sollte es wichtig sein, welche Atome "überleben"; si sind doch alle gleich und gleichwertig.Halman hat geschrieben:Ähnlich verhält es sich mit einem radionaktiven Isotop. Zwar ist die Halbwertzeit bestimmbar, aber der Zerfall eines einzelnen Atoms geschiet vollkommen zufällig.
Der mathematische Formalismus funktioniert hervorragend, also genau das, was ich NICHT verstehe.Pluto hat geschrieben:Das stimmt.Halman hat geschrieben:Diesen widerspricht die Quantenmechanik jedoch sehr hartnäckig. Um es mal scherzhaft auszudrücken: Quantenobjekte scheinen sich für den gesunden Menschenverstand nicht zu interessieren.
Obwohl etwa 70% der weltweiten Industrieproduktion Quanteneffekte verwendet, wissen noch sehr wenig darüber was sich wirklich in diese sub-nano Welt abspielt.
Gut möglich. Aber der Mensch kann immer weiter grübeln und forschen.Pluto hat geschrieben:Wir können die Quantenwelt statistisch erfassen. Das ist in meinen Augen erstens schon sehr viel und vermutlich auch die einzige Möglichkeit sie zu erklären.Halman hat geschrieben:Gem. der Quantenmechanik (QM) lässt sich das Verhalten von Quantenobjekten nicht eindeutig bestimmen, ihr Verhalten ist objektiv zufällig (die Schrödingergleichung erlaubt lediglich eine statistische Wahrscheinlichkeit zu berechen).
Nun, dann bin ich gespannt, was Agent Scullie dazu sagt. Vielleicht hat es etwas mit dem Unruh-Effekt zu tun, den er in diesem Beitrag erwähnte.Pluto hat geschrieben:Unsere experimentellen Mittel sind aber auch filigran geworden. Siehe den dynamischen Casimir-Effekt, wo Licht aus dem Nichts erzeugt wird.Halman hat geschrieben:Die Wellenfunktion erweist sich als außgesprochen "filigranes Gebilde" (bitte nicht wörtlich nehmen, hier bediene ich mich einer anschaulichen Sprache), sie zerplatzt wie eine Seifenblase, sobald wir sie durch Beobachtung/Messung antasten.
Energie wird durch die Schwingungen des Spiegels von Außen ins System gepumpt, weshalb die virtuellen Photonen sich in Reale verwandeln können und nicht wieder ins Nichts zurückfallen - so erklärt es der Physiker in dem von mir verlinkten Video.
Agent Scullie hat geschrieben:"Nach der QFT besitzen alle Felder einen Vakuumzustand. Ist ein schwarzes Loch in der Nähe, so wird durch dessen Gravitationsfeld der Vakuumzustand in einer Weise modifiziert, dass Teilchen entstehen, die von einem Beobachter außerhalb des schwarzen Loches als Hawking-Strahlung registriert werden können. Einen ganz ähnlichen Effekt gibt es auch ganz ohne schwarzes Loch und ohne Gravitationsfeld, nämlich bei einem beschleunigten Beobachter in einer flachen Raumzeit, den sog. Unruh-Effekt: was von einem gleichförmig bewegten Beobachter als Vakuumzustand registriert wird, wird von einem beschleunigten Beobachter als Zustand mit Teilchen wahrgenommen."
Sie bilden gewissermaßen einen makroskopischen "Atomkern" aus Neutronen. Soweit ich dies verstehe, wirkt auch da das Pauli-Prinzip, denn der Neutronenstern hat ja ein Volumen. Darum wirkt wohl der Entartungsdruck (auch: Fermi-Druck), allerdings habe ich dies nicht so recht verstanden.Pluto hat geschrieben:Da fehlt was.Halman hat geschrieben:Die Fermionen unterliegen dem Pauli-Prinzip. Dieses Prinzip ist dafür verantwortlich, dass sich in der K-Schale der Atome² nur zwei Elektronen mit gegensätzlichen Spin befinden können. Ein drittes Elektron hätte wieder den selben Spin wie eines der anderen und dieses duldet das Pauli-Prinzip nicht.
Neutronen sind Fermionen, aber ein Neutronenstern besteht aus Trillionen von Neutronen, oder nicht?
Ich erinnere mich an eine Diskussion mit Agent Scullie über braune Zwerge - ziemlich schwerer Stoff.
@Agent Scullie
Du bist einfach unentbehrlich.
Seeadler bittet um Deine Mitwirkung:
Zitat von seeadler:
(Und ja, es wäre natürlich schön, wenn sich @Agent Scullie ebenfalls an der Diskussion beteiligen würde)
Tja, ein Proton müsste man sein: Dann würde man die Quantenphysik verstehen, wäre immer positiv drauf und hätte eine nahezu unendliche Lebenszeit:-) - Silvia Arroyo Camejo
#187 Re: Quantenmechanische Gedanken zum Urknall
Es ist wichtig, was ein einzelnes Atom macht, weil wir es experimentell beobachten können, z.B. in einer magnetischen Falle.Halman hat geschrieben:Das mag sein, dennoch gilt der Interdeterminsmus der skurrilen Quantenwelt. Dies ist naturphilosophisch meiner Meinung nach von größter Bedeutung.Pluto hat geschrieben:Wir können die Halbwertszeit exakt angeben. Warum sollte es wichtig sein, welche Atome "überleben"; si sind doch alle gleich und gleichwertig.Halman hat geschrieben:Ähnlich verhält es sich mit einem radionaktiven Isotop. Zwar ist die Halbwertzeit bestimmbar, aber der Zerfall eines einzelnen Atoms geschiet vollkommen zufällig.
Das Grundproblem ist, dass sich Theorie und Erfahrung (Experiment) hier voneinander abgespalten haben. Die Theorie arbeitet mit Wellenfunktionen, abstrakten Gebilden, die man als Wahrscheinlichkeitsverteilungen bezeichnen kann. Diese haben in der Theorie den Wirklichkeitsaspekt, sie sind das, was im Kern des Models steckt.
Aber es ist nicht das, was wir beobachten. Wir beobachten Teilchen oder Wellen, wir beobachten Orte und Impulse, Zeit und Energie. Das ist es, was für uns real ist.
Das Bilden von Erwartungswerten ist die mathematische Abbildung zwischen den Welten. Aber dabei geht etwas verloren, nämlich die Vorhersagbarkeit. Ich kann für ein einzelnes, beobachtbares Objekt keine Vorhersage mehr machen, die keine Wahrscheinlichkeit ist. Also weiß ich schlicht nicht, was in Zukunft passiert, bis es passiert. Ich weiß nur, ob ich gespannt warten darf oder mich in Geduld fassen sollte. Aber selbst dann könnte ich enttäuscht werden, denn auch ein Atomkern, der eine Halbwertszeit von Sekunden hat, wartet vielleicht ein paar Jahre mit dem Zerfall.
Praktisch hat dieses Problem kaum Auswirkungen, aber für die Naturphilosophie ist das eine massive Änderung gegenüber früherem Denken.
Gott würfelt nicht, meinte Einstein. Aber er irrte. Gott nutzt den Zufall - jeden Tag.
#188 Re: Quantenmechanische Gedanken zum Urknall
Du legst den Finger in die Wunde der Quantenphysik. Wir können offenbar nicht anders als in unserer Welt denken.ThomasM hat geschrieben:Es ist wichtig, was ein einzelnes Atom macht, weil wir es experimentell beobachten können, z.B. in einer magnetischen Falle.
Das Grundproblem ist, dass sich Theorie und Erfahrung (Experiment) hier voneinander abgespalten haben. Die Theorie arbeitet mit Wellenfunktionen, abstrakten Gebilden, die man als Wahrscheinlichkeitsverteilungen bezeichnen kann. Diese haben in der Theorie den Wirklichkeitsaspekt, sie sind das, was im Kern des Models steckt.
Aber es ist nicht das, was wir beobachten. Wir beobachten Teilchen oder Wellen, wir beobachten Orte und Impulse, Zeit und Energie. Das ist es, was für uns real ist.
Die Quantenwelt scheint sich nicht darum zu scheren, also sind wir allein auf statistische Mittel angewiesen, wollen wir sie versuchen zu verstehen.
Das ist das kuriose an diesen Phänomenen: Wir können sie nur unter Zuhilfenahme der Wahrscheinlichkeit, oder mit (lahmen) Begriffen wie Superposition erklären.ThomasM hat geschrieben:Ich kann für ein einzelnes, beobachtbares Objekt keine Vorhersage mehr machen, die keine Wahrscheinlichkeit ist. Also weiß ich schlicht nicht, was in Zukunft passiert, bis es passiert. Ich weiß nur, ob ich gespannt warten darf oder mich in Geduld fassen sollte. Aber selbst dann könnte ich enttäuscht werden, denn auch ein Atomkern, der eine Halbwertszeit von Sekunden hat, wartet vielleicht ein paar Jahre mit dem Zerfall.
Ja. Die Quantenwelt scheint sich unserem gewohnten Denken zu entziehen.ThomasM hat geschrieben:Praktisch hat dieses Problem kaum Auswirkungen, aber für die Naturphilosophie ist das eine massive Änderung gegenüber früherem Denken.
Doch in der Praxis verstehen wir eine ganze Menge davon, wenn man sich vor Augen führt dass mittlerweile 70% des Industrieausstoßes in irgendeiner Form die QM für ihre Technik nutzt.
Der Naturalist sagt nichts Abschließendes darüber, was in der Welt ist.
#189 Re: Quantenmechanische Gedanken zum Urknall
Nein. Bei einer Positionsmessung findet eine Streuung statt, dadurch wird die Phase gestört.Halman hat geschrieben:So verschwindet beim Doppelspaltexperiment das Interferenzmuster, sobald man durch die Messung die Positionen der Quantenobjekte bestimmt. Dass lässt sich dadurch erklären, dass durch die Messung die Wellenfunktion des Quantenobjektes kollabiert.
Nochmal: Die Kopenhagener Deutung lautet:Halman hat geschrieben:Bei der Messung (z. B. auf dem Detektorschirm) kollabiert nach der Kopenhagener Deutung diese Wellenfunktion
W(x) = |psi(x)|²
Die Wahrscheinlichkeitsdichte = Betragsquadrat der Wellenfunktion.
Nochmal:
W(x) = |psi(x)|²
Die Wahrscheinlichkeitsdichte = Betragsquadrat der Wellenfunktion.
Nochmal: Eine Wahrscheinlichkeit ist eine statistische Aussage. Es ist schwachsinnig, eine statistische Aussage auf Einzelfälle anzuwenden.
Nochmal: Es ist schwachsinnig, eine statistische Aussage auf Einzelfälle anzuwenden.
#190 Re: Quantenmechanische Gedanken zum Urknall
So ist es!Janina hat geschrieben:Es ist schwachsinnig, eine statistische Aussage auf Einzelfälle anzuwenden.
Der Naturalist sagt nichts Abschließendes darüber, was in der Welt ist.