Pluto hat geschrieben:Nun zum eigentlichen Gedankenexperiment.
Man denke sich die Gasteilchen ganz weg und wiederholt das Experiment ohne Teilchen. Die Logik sagt uns, die Hälfte von Nichts ist nichts.
Kein Problem, oder?
Heute wissen wir aber dank dem
Casimir-Effekt, dass selbst das Nichts (Vakuum) mit Energie gefüllt ist, weil ständig virtuelle Teilchen entstehen und verschwinden (und die müssen ja irgendwo her kommen). Man nennt das auch das "brodelnde" Quantenvakuum. Was geschieht nun mit dieser Quantenenergie wenn wir den Inhalt von Nichts verdoppeln? Bleibt die Energie konstant oder ist doppelt so viel drin wie zuvor?
Beim Casimir-Effekt treten nach meiner Kenntnis KEINE virtuellen Teilchen auf. Die treten meines Wissens nur bei Wechselwirkunngen von Quantenfeldert auf. Ein Beispiel wäre hierfür der β-Zerfall.
Bei Feynman-Diagrammen gilt die Energieerhaltung insofern, dass die Gesamtenergie der Teilchen vor der Wechselwirkung (der "Knick" im Diagramm) identisch mit der Gesamtenergie nach der Wechselwirkung ist.
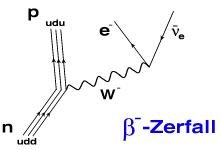 Feynman-Diagramm-Quelle
Feynman-Diagramm-Quelle
Am Anfang der Wechselwirkung ist ein Neutron mit 940 MeV, am Ende ein Proton mit 938 MeV, sowie zwei Leptonen (Elektron und Antineutrino mit insgesamt Leptonenzahl 0), die zusammen mit dem Proton der Energie des Neutrons entsprechen (ich weiß, dass die Zahlen nicht genau sind).
Das meiner Meinung nach Bemerkenswerte bei diesem Diagramm ist, dass der innere Graf ein W-minus-Boson mit
80 GeV beschreibt, bei dem es sich um ein virtuelles Eich-Boson der schwachen Wechselwrkung handelt. Offenkundig sind 80 GeV ca. 85 mal mehr Energie als 940 MeV. Doch dieser Wert tritt nur in der Wechselwirkung innerhalb des inneren Grafen auf (Beteiligung eines Quantenfeldes). Am Anfang und Ende des Feynman-Diagrammes gilt die Energieerhaltung. Dieser quantfeldtheoretischer Sachverhalt ist für mich äußerst rätselhaft.

Beim Casimir-Effekt treten hingegen KEINE virtuellen Teilchen auf, es handelt sich lediglich um Vakuumfluktuatationen, also um die Unschärfe der Feldstärke der immateriellen Quantenfelder, welche gemäß der Quantenfeldtheorie (GFT) den gesamten Raum erfüllen. Diese Felder werden meiner Meinung nach in der Öffentlichkeit aufgrund der Nachlässigkeit in der Populärwissenschaft noch viel zu wenig als physikaische "Objekte", die etwas bewirken können, erkannt (es müssen nicht immer Teilchen beteiligt sein).
Durch die Metallplatten werden die möglichen Vakuumfluktuatationen beschränkt und damit die Energiedichte gesenkt. Nun ist es aber so, dass die Energiedichte des echten Vakuums null ist, womit sie beim Casimir-Effekt negativ wird. Da die QFT allerdings meinen bescheidenen Horizont bei weitem übersteigt, verweise ich auf die fachliche Erklärung meines "Mentors":
Zitat von
Agent Scullie:
Der übliche Ansatz zur Beschreibung des Quantenvakuums ist der, dass man jedes Quantenfeld in Moden zerlegt und jede Mode wie einen quantenmechanischen hamonischen Oszillator behandelt. Dabei kommt heraus, dass im Vakuumzustand jede Mode die Energie h*f/2 hat, wobei f die Frequenz der Mode ist. Allerdings führt das zu dem Resultat, dass die Energie des Vakuumzustandes unendlich groß ist, da es unendlich viele Moden gibt. Mehr noch: nicht nur die gesamte Energie des Vakuumzustandes im gesamten Universums ist unendlich, sondern auch die Energiedichte, weil schon dann, wenn man nur ein endliches Raumvolumen betrachtet, unendlich viele Moden beitragen.
Dieses unschöne Resultat kann man dadurch umgehen, dass man den Energienullpunkt umdefiniert. Statt h*f/2 hat dann jede Mode im Vakuumzustand die Energie 0. Wenn dann aber wie beim Casimir-Effekt ein Teil der Moden unterdrückt wird und die Gesamtenergie des Vakuumzustandes kleiner ist als sonst üblich, hat das den Effekt, dass die Energie des Vakuumzstandes negativ wird.
Pluto hat geschrieben:Doppelt so viel Energie...?
Wie kann das sein, wo doch nach dem ersten Satz der Thermodynamik, Energie weder geschaffen, noch zerstört werden kann?

Nehmen wir nun das Universum...
In einem statischen Universum geschieht erst mal nichts. Die moderne Kosmologie geht heute aber von einem
expandierenden Universum aus.
Was geschieht nun mit der dunklen Energie die das Universum durchzieht? Bleibt diese Energie konstant, oder vergrößert sie sich nicht ständig?
Mein Eindruck ist, dass die Energieerhaltung nur dann uneingeschränkt gilt, wenn der Raum staatisch ist. Die einsteinischen Feldgleichungen zeigen, dass die Energiedichte an der Geometrie der Raumzeit gekoppelt ist. Vielleicht gibt es eine Kopplung zwischen Energie und Raum oder Raumzeit.

(s.
Der Rand eines Randes ist Null .)
Die CMB besteht überwiegend aus MW-Photonen. Doch im Anfang des Universums war ihre durchschnittle Frequenz ("Temperatur") viel höher. Im frühen Universum bestand die CBM aus hochenergetischen γ-Quanten.
In der Grafik ist die CMB als Hyperfläche der dargestellten Raumzeit des Universums zu sehen, ca. 380.000 Jahre nach dem "Urknall". Damals lag die Temperatur des Universums bei 3000° K. Doch zeither expandierte der Raum und die durschnittliche Frequenzt der CMB sank weiter ab.
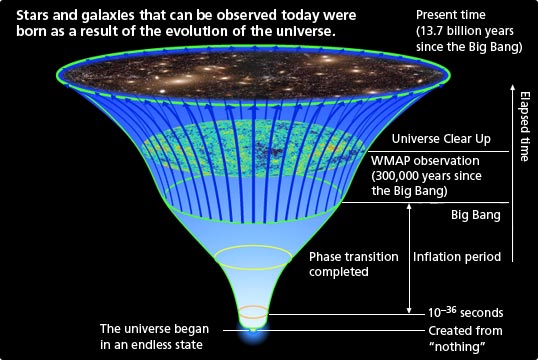 Grafikquelle
Grafikquelle
Licht lässt sich als EM-Welle beschreiben. Nun stelle Dir mal vor, man würde den Raum kontrahieren, dann würde man damit auch die EM-Welle wie eine "Feder" zusammenstauchen. Die Frequenz steigt und gem. E=h
ν nimmt damit die Energie des Lichtes zu.
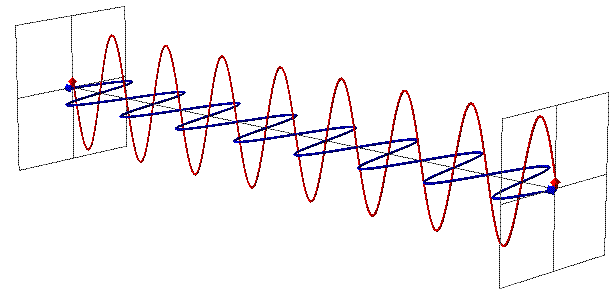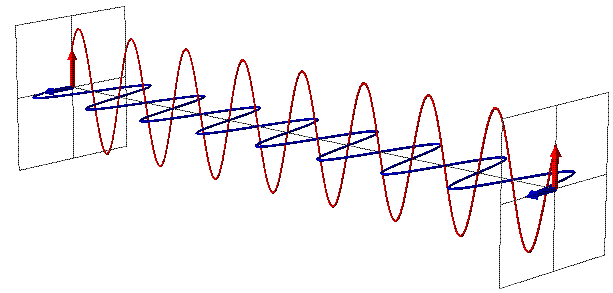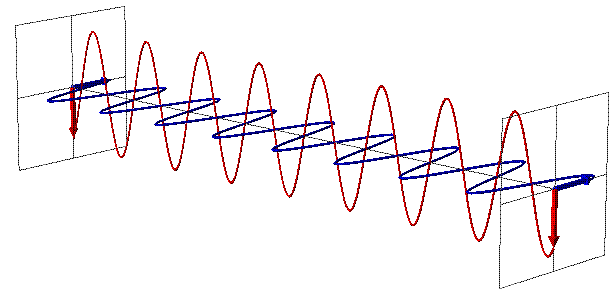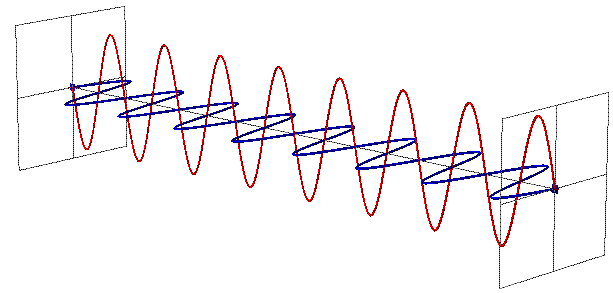 Animations-Quelle
Animations-Quelle
Umgekehrt, wenn der Raum expandiert, wird die EM-Welle wie eine "Feder" auseinandergezogen. Die Frequenz sinkt und die Energie des Lichtes fällt.
Agent Sullie sagte mir mal: "
Energie ist in der ART - und ganz besonders in deren kosmologischen Lösungen - eine äußerst nichttriviale Angelegenheit." (Der verlinkte Beitrag lohnt sich für Physik-Initeressiere zu lesen.)
Von ihm ist auch die PDF-Datei über
die Divergenzfreiheit des Energie-Impuls-Tensors. Später erklärte er mir ergänzend Folgendes:
Zitat von
Agent Scullie:
Dass die Divergenz des Energie-Impuls-Tensors null ist (der Energie-Impuls-Tensor also divergenzfrei ist), ist das ART-Pendant dafür, dass die Energie lokal erhalten bleibt. Das habe ich im Dokument auch an einem Beispiel erläutert: nimm zunächst eine flache Raumzeit und eine ideale Flüssigkeit in dieser, die räumlich homogen verteilt ist, d.h. bei der Druck und Energiedichte überall im Raum gleich ist. In einem Inertialsystem hat der Energie-Impuls-Tensor dieser idealen Flüssigkeit dann die Gestalt
T^ij = diag(rho, p, p, p)
mit den Diagonalelementen
T^00 = rho, T^11 = T^22 = T^33 = p
Die Nichtdiagonalelemente T^ij mit i != j sind alle null. Aufgrund der räumlichen Homogenität verschwinden die Ableitungen der Komponenten des Energie-Impuls-Tensors nach den räumlichen Koordinaten:
d T^ij / dx^1 = 0
d T^ij / dx^2 = 0
d T^ij / dx^3 = 0
Die Divergenz des Energie-Impuls-Tensors ist nun (in einer flachen Raumzeit in einem Inertialsystem) gerade gegeben durch
d T^ij / dx^i = d T^0j / dx^0 + d T^1j / dx^1 + d T^2j / dx^2 + d T^3j / dx^3
Da die drei räumlichen Ableitungen null sind, bleibt nur
d T^ij / dx^i = d T^0j / dx^0
übrig. Da der Energie-Impuls-Tensor außerdem diagonal ist, muss j=0 sein:
d T^ij / dx^i = d T^00 / dx^0
Da x^0 die Zeitkoordinate ist, ist das nichts anderes als die Ableitung der Energiedichte nach der Zeit, also die Änderung der Energiedichte pro Zeiteinheit. Wenn nun die Energie erhalten bleibt, muss die Energiedichte zeitlich konstant sein (wir haben ja keine räumlichen Energieflüsse, die sich in Nichtdiagonalelementen des Energie-Impuls-Tensors zeigen würden). Es muss also d T^00 / dx^0 = 0 gelten. Und das ist gerade gleichbedeutend damit, dass
d T^ij / dx^i = 0 gilt
also die Divergenz des Energie-Impuls-Tensors null ist. Wäre die Divergenz ungleich null, so müsste sich die Energiedichte mit der Zeit ändern, und folglich die Energieerhaltung verletzt sein.
Nun brauche ich nur noch einen fachkompeteneten User, der mir dieses Fachchinesisch "übersetzt"?



