seeadler hat geschrieben:Trotzdem, lieber halman, habe ich nach wie vor ein problem, mir jene "Raumzeitkrümmung" vorzustellen..
Auf YouTube habe ich eben eine schönes Video gefunden, dass hoffentlich ein wenig hilft, sich die Raumkrümmung besser vorstellen zu können.
Es sei darauf hingewiesen, dass sowohl in 2D-Grafiken und Animation wie auch in 3D-Bildern und Animationen lediglich der
Raumteil der Raumzeit dargestellt wird.
Um die raumzeitliche Krümmung vierdimensional zu verstehen, ist eine andere Betrachtung notwendig. Auf Wunsch werde ich mich dazu noch äußern.
seeadler hat geschrieben:Es ist für mich an dieser Stelle leichter, wenn ich hier genau das einbeziehe, was du auszuklammern versuchst : Die Expansion!
Okay, reden wir über die Expansion des Universums. Grundsätzlich ist es auch möglich ein statisches Unviversum gem. der ART zu beschreiben, in denen Massen Gravitatinsfelder erzeugen. Ob Expansion, statischesches Gleichgewicht oder Kontraktion, dies würde an den Naturgesetzen und den Zeitpfeil meiner sehr bescheidenen Kenntnis nach nichts verändern.
Da die Energiedichte des Universums zweifelsfrei positiv ist (dunkle Materie, baryonische Materie, CMB), kann die Expansion gem. den einsteinischen Feldgleichungen der ART nur durch negativen Druck der Druckkomponenten des Energie-Impuls-Tensors versucht werden.
In diesem Energie-Impuls-Tensors ist die Energiedichte Ï und 3
p (Druck) enthalten: Daran ist die Metrik der Raumzeit gekoppelt. Wie bereits erwähnt, erklärt W. Thirring in seinem Buch
Kosmische Impressionen das einstein'sche Gravitatiosnfeld auf Seite 43 folgendermaßen:
Dieses Feld wird durch ein quadratisches Schema mit vier Zeilen und vier Spalten (eine Matrix oder Tensor 2ter Stufe) beschrieben. Von seinen 4 x 4 = 16 Komponenten sind allerdings nur 10 voneinander unabhängig und jede hat seine eigene Quelle. In der entsprechenden Quellenmatrix ist die Energiedichte (das wir auch mit E bezeichnen) die größte Komponente.
Für gewöhnlich ist die Energiedichte die größte Komponente, wenn es darum geht, Gravitationsfelder von Massen, wie Sternen, Planeten oder interstellaren Nebeln zu beschreiben. Es gibt aber auch Fälle, in denen der Druck eine viel größere Rolle spielt und zwar dann, wenn die Dichte extrem hoch ist. Dies ist insbesondere bei Schwarzen Löchern der Fall und im "Uratum" (Lemaître), aus dem unser Universum theoretisch hervorging.
Thirring leitet direkt im Anschluss an obigen Zitat für sein Buch
E + 3
p zur Beschreibung des Gravitatiosnfeldes ab. Ist der Druck negativ und hinreichend groß, wenn also global-kosmologisch (
E-3p vorliegt und der negative Teil überwiegt), expandiert das Universum.
Bereits Albert Einstein vermutete eine der Gravitation entgegengesetzte Kraft. Daher fügte er seiner ART-Feldgleichung die
Kosmologische Konstante in Form eines Λ-Terms hinzu, um das von ihm seinerzeit favorisierte ästhetisch schöne, statische Universum plausibel erklären zu können. Als dann Edwin P. Hubble die Rotverschiebung ferner Galaxien beobachtete, die auf ein expandierendes Universum hinwies, verwarf er diese Idee als seine größte Eselei und setzte den Λ-Term auf 0.
Folgende einsteinische Feldgleichung sieht etwas komplizierter aus als die, die ich vor kurzem hier gepostet hatte, weil sie die Kosmologische Konstante
Λ enthält.
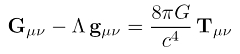
Dabei wird
Λ mit dem metrischen Tensor
gμν multipiziert. Ist
Lambda positiv, überwiegt die Antigravitation, ist
Λ negativ, überwiegt die Gravitation.
Als dann 1998 die Beobachtung ferner Supernovae vom Typ Ia (dessen absolute Leuchtkraft meines Wissens näherungsweise bekannt ist) darauf schließen ließ, dass unser Universum in den letzten 5 bis 6 Milliarden Jahren zu unserer Überraschung beschleunigt expandiert, erinnerte man sich an den Λ-Therm, den Einstein auf 0 gesetzt hatte. Nach aktuellen Messungen scheint der Wert für den Λ-Term bei 0,683 zu liegen. Hierfür wurde der Begriff
Dunkle Energie geprägt. Die beschleunigte Expansion wird also dadurch erklärt, indem ΩΛ ≈ 0.683 gesetzt wird, d.h. dass etwa 68,3% des Universums aus Dunkler Energie besteht.
Wie kam Einstein überhaupt darauf, dass bei Gravitationsfeldern die Geometrie der Raumzeit gekrümmt sein müsse? Zur Erklärung empfehle ich Dir wärmstens sein Buch
Über die spezielle und die allgemeine Relativitätstheorie. Darin erklärt Einstein Herleitungen, die ich sonst NIRGENDS erklärt bekam. Er geht auch auf die Thematik Raum, Zeit und Raumzeit ein.
Ich empfehle Dir den Link:
https://archive.org/stream/berdiespezie ... g_djvu.txt
Bitte scrolle etwa zwei Drittel bis zu "§ 23" herunter:
I § 23. Verhalten von Uhren und Maßstaben auf einem
I ^ rotierenden Bezugskörper.
Dieser Abschnitt ist immens wichtig!!!
Vereinfacht gesagt, könnte ein Beobachter auf einer großen Kreisscheibe mit recht behaupten, sich in einem Gravitationsfelde zu befinden, welchers ihn nach außen "zieht".
Offenkundig bewegt sich der äußerste Teil der Kreisscheibe am Schnellsten. Wenn sich die Gesetze der Längenkontraktion und Zeitdilatation der SRT auch auf rotierende Bezugssysteme verallgemeinern lassen, dann sollte der Umfang des Kreises kontrahiert sein. Die Kontrakton erfolgt nur in Bewegungsrichtung, der Umfang ist also nicht betroffen!
Nun wissen wir aber ganz genau, dass Umfang und Durchmesser von Kreisen gem. geometrischer Logik ein fixes Verhältnis von 1:Ï€ haben. Was passiert nun? Reiß die Kreisscheibe von außen ein? Dies entspricht offenkundig nicht unserer Erfahrung.
Einstein gelang es, das geometrische Problem zu lösen. Die einzige Möglichkeit besteht darin, anstelle von kartesischen Koordinaten auf gauß'sche Koordinaten zu wechseln, mit denen sich beliebig gekrümmte Räume darstellen lassen. Würde sich die Kreisscheibe zu einer Art "Schüssel" krümmen, könnte der Umfang kontrahieren und dabei der Durchmesser unverhändert bleiben.
Die Schüssel soll hier nur zur Veranschauchlichung dienen, denn eben habe ich eine weitere IMAGINÄRE Raumdimension hineingeschuggelt, in dem ich die Kreisscheibe "eingebettet" habe. Diese Einbettungsdimension GIBT ES NCIHT! Was nun? Am besten führen wir uns vor Augen, dass die darstellung mit der äußeren Krümmung lediglich als Veranschauclichung dient, die unserem Vorstellungsvermögen entgegenkommt, aber leider zu den Fehlschluss verleitet, sich eine weitere Raumdimension zu denken.
Gauß'sche Koordinaten kommen ganz ohne äußere Krümmung und Einbettungsdimension aus. Damit ist es möglich, eine innere Krümmung zu beschreiben.
Darüber hatten wir uns schon mal unterhalten. Vielleicht erinnerst Du dich an Folgendes:
Im Gegensatz zum starren kartesischen Koordinatensystem sind gaußsche Koordinaten für beliebig gekrümmte Räume und Raumzeiten verwendbar. Ich vermute, dass deswegen die Wahl des Koordinatensystems in der ART beliebig ist. Wenn Du magst, schau doch bitte, was Albert Einstein hierüber in seinem
berühmten Essay schrieb.
Warum sollte die raumzeitliche Krümmung nur für ein spezielles "Gravitationsfeld" eines rotierdenen Bezugsystems gelten, wenn das Äquivalenzprinzip gelten soll? Daher erscheint es sinnvoll, ganz allgemein davon auszugehen, dass die Raumzeit in Gravitationsfeldern gekrümmt ist. Diese Idee ist genial, denn es stellte sich heraus, dass die Gravitation selbst geometrisch erklärt werden konnte.