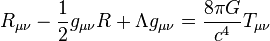ThomasM hat geschrieben:Tensoren sind ein recht kompliziertes mathematisches Werkzeug. Auf dem Niveau, auf dem wir hier diskutieren, spielt die genaue mathematische Bedeutung kaum eine Rolle.
Das sehe ich auch so, zumal Du dann hier nur noch mit Janina, Pluto und Zeus fachsimpeln könntest.

ThomasM hat geschrieben:Man muss nur daran denken, dass man eine Gleichung, wie die der ART nicht einfach mit Dreisatz behandeln darf. Es handelt sich um eine abgekürzte Schreibwewise für 16 gekoppelte Differentialgleichungen.
Gruß
Thomas
Danke für die Erkärung, die ist für mich sehr aufschlussreich (noch ein Puzzelteil aus meiner Sicht).
Hier wurde ja schon erwähnt, dass die Tensoren Differentialgleichungen enthalten, allerdings konnte ich diese Information nicht verarbeiten.
Aus Wheelers Buch
"Gravitation und Raumzeit" konnte ich entnehmen, dass die Infinitesimalrechnung für die einsteinischen Feldgleichungen von zentraler Bedeutung ist. 16 gekoppelte Differentialgleichungen zur Beschreibung der Metrik sind natürlich sehr komplex.
Da ich dies mathematisch nicht nachvollziehen kann, begnüge ich mich mit einer laienhaften naturphilosphischen Betrachtung. Damit fehlt mir zwar das exakt-naturwissenschaftliche Verständnis, aber ein qualitatives Grundverständnis ist besser als Nichts. Bei aller Bescheidenheit kann ich immerhin herleiten, dass die Metrik der Raumzeit an Energiedichte Ï und Druck 3
p gekoppelt ist und zwar unabhängig davon ob Ï massebehaftet ist. Ich fasse zusammen: Die
Metrik der Raumzeit gibt ihre Geometrie an und Gravitation wird gem. der ART sinnvollerweise über eine geometrische Funktion beschrieben, denn Gravitation
ist die
Krümmung der Raumzeit.
In meinem Buch
Kosmische Impressionen wird dies von Prof. W. Thirring angerissen:
Zitat von Prof. Walter Thirring aus Kosmische Impressionen (Seite 43):
Dieses Feld wird durch ein quadratisches Schema mit vier Zeilen und vier Spalten (eine Matrix oder Tensor 2ter Stufe) beschrieben. Von seinen 4 x 4 = 16 Komponenten sind allerdings nur 10 voneinander unabhängig und jede hat seine eigene Quelle. In der entsprechenden Quellenmatrix ist die Energiedichte (das wir auch mit E bezeichnen) die größte Komponente.
Im folgendem Text leitere Thirring die Formel
E + 3p ab.
E steht hier vereinfach für die Energie. Jedes Massezentrum repräsentiert gem.
E=mc² Energie
Inwiefern sind 10 der 16 gekoppelten Differentialgleichungen voneinander unabhängig? Welche Quellen haben sie? Gehören dazu die Strömungen der Energiedichte (wie z.B. die Magmaströmungen), die Temperatur und magnetisches Feld?
In der "Matrix" mit den 16 Komponenten sind in der Tensor-Formel (s. u.) 12 Komponenten auf 0 gesetzt. Eine Komponente ist die
Energiedichte Ï und drei Komponenten sind der
Druck 3
p.
In Thirrings Formel (die er für sein populärwissenschaftliches Buch entwickelt hat) steht
E für Ï. In Wikipedia habe ich die Schreibweise
Ïc² gesehen:
 Formelquelle
Formelquelle
Darf ich
E =
Ïc² schreiben? Darf ich sagen, dass Geometrie der Raumzeit (also die Gravitation) an
Ïc² + 3p gekoppelt ist?
Wenn nun jemand nach dem "Mechanismus" für die Gravitation fragt (@seeadler beschäftigt offenbar diese Frage), müssen wir das konstatieren, dass dieser leider nicht in den einsteinischen Feldgleichungen beschrieben wird, oder übersehe ich hier etwas Wichtiges?
@seealder
Da hier u.a. auch über das sehr bedeutsame
Äquivalenzprinzip gesprochen wurde, verlinke ich an dieser Stelle ein mMn sehr aufschlussreiches Essay in Form eines 72-seitigen PDF-Dokumentes:
Äquivalenzprinzip & Schleifen-Quantengravitation. Darin wird u.a. erklärt:
Zitat aus Einsteins Äquivalenzprinzip (Seite 18-19):
In der ART ist die Reaktion von Körpern auf Gravitationseinwirkung rein geometrisch erklärt – Massen verzerren die Geometrie von Raum und Zeit, und alle Körper folgen den geradestmöglichen Bahnen in dieser verzerrten Raumzeit. Daß alle Körper in einer gegebenen Situation die gleiche Fallbeschleunigung erfahren, liegt daran, daß ihre Bewegung direkt von den Eigenschaften der sie umgebenden Raumzeit bestimmt wird
... Insgesamt ist Gravitation ein Aspekt der Geometrie von Raum und Zeit.
Zum Äquivalenzprinzip
Nimm an, Du sitzt in einer Kabine ohne Fenster, Du hast also keine Möglichkeit etwas über die Außenwelt zu erfahren. Bälle fallen darin zu Boden und Du hast Gewicht. Befindet sich die Kabine auf der Erde oder in einer Rakete im Weltraum, die beschleunigt? Beides wäre möglich, da beide Fällle äquivalent sind (Äquivalenzprinzip).
Wenn die Raketentriebwerke ihre Arbeit einstellen, würden Bälle in der Kabine nicht mehr zu Boden fallen, auch Dein Gewichtszustand wäre augenblicklich beendet. Dieser Fall ist äquivalent mit dem freien Fall einer Kabine. Auch hier ist es unmöglich einen Unterschied festzustellen - es gilt Einsteins Äquivalenzprinzip.
@Zeus
Danke für den Link.